What is in common between finding the closest parking lot, optimizing delivery stops order, or calculating a service area? A straightforward yet correct answer could be - all three problems are related to maps, routing, and optimization.
What is less obvious is that they all depend on one very important, yet often invisible component - the route matrix.
What is route distance matrix
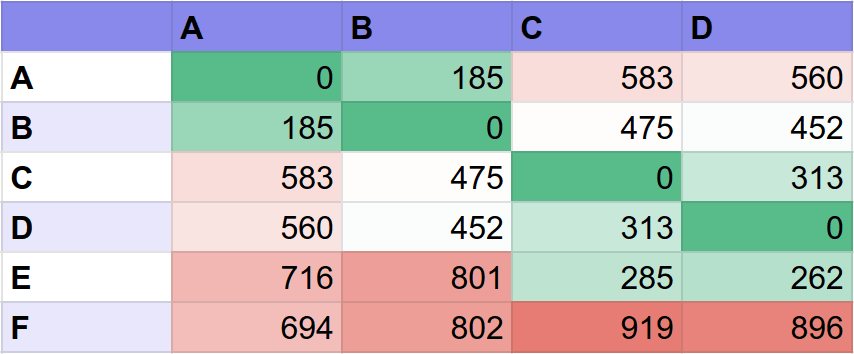
In essence, a route matrix is a table that summarizes travel "cost" - usually time or distance - between one or more source and destination locations. Because of this, it is sometimes also called a "distance matrix", "time-distance matrix", "drive time matrix" or "cost matrix".
Normally, each source location is represented by a row, and each destination is represented by a column:
| SOURCE / DESTINATION | DESTINATION 1 | DESTINATION 2 |
|---|---|---|
| SOURCE A | A -> 1 | A -> 2 |
| SOURCE B | B -> 1 | B -> 2 |
Route matrix calculation requires finding all possible route combinations between all sources and all destinations. Even for a relatively small scenario containing just 5 sources and 10 destination locations we need to calculate 5 sources * 10 destinations = 50 routes.
Because of this, calculation of a route matrix can be very computationally expensive and can take from a fraction of a second to a few hours.
How to use distance matrix
You may wonder - how this table could help to solve real-world problems? And rightfully so - route distance matrix would be nearly useless without smart algorithms that take it as an input and calculate the results we need.
Some widely used examples include the Dijkstra algorithm for finding optimal routes between multiple locations and the Ramer-Douglas-Peucker algorithm for calculating isolines and service areas.
Such algorithms are so common and useful, that nowadays you do not need to be a mathematician, engineer, or programmer to use them. They are already implemented in many products that you likely to use daily - from maps app in your phone, to spreadsheets like Excel or Google Sheets, and of course inside our Location Platform and APIs.
So, if matrix calculations are already hidden "inside" most products, why would you want to use the distance matrix directly? Because of its flexibility! Existing products and APIs may not be able to do exactly what you need, or you may be building another great product that uses it under the hood.
Distance matrix for route optimization
Finding the shortest route for two or more locations is likely one of the most frequently solved optimization problems. We depend on it every day when driving with GPS navigation or checking a route on Google Maps.
But most apps, including Googe Maps, only allow optimizing for the shortest route time. Sometimes it can be necessary or desirable to optimize for distance or other criteria.
Let's take a look at the example below - a route with four locations, and optimize it for the shortest total distance.
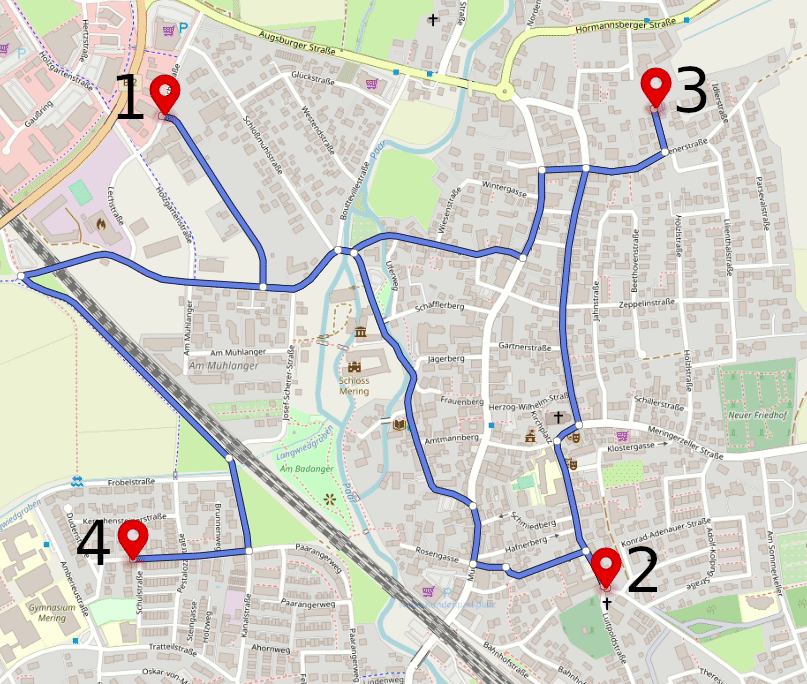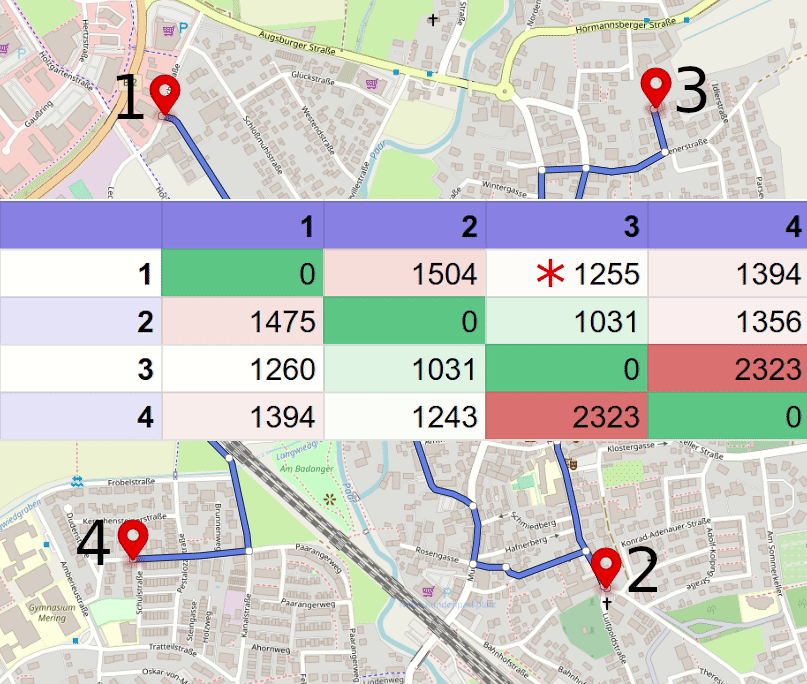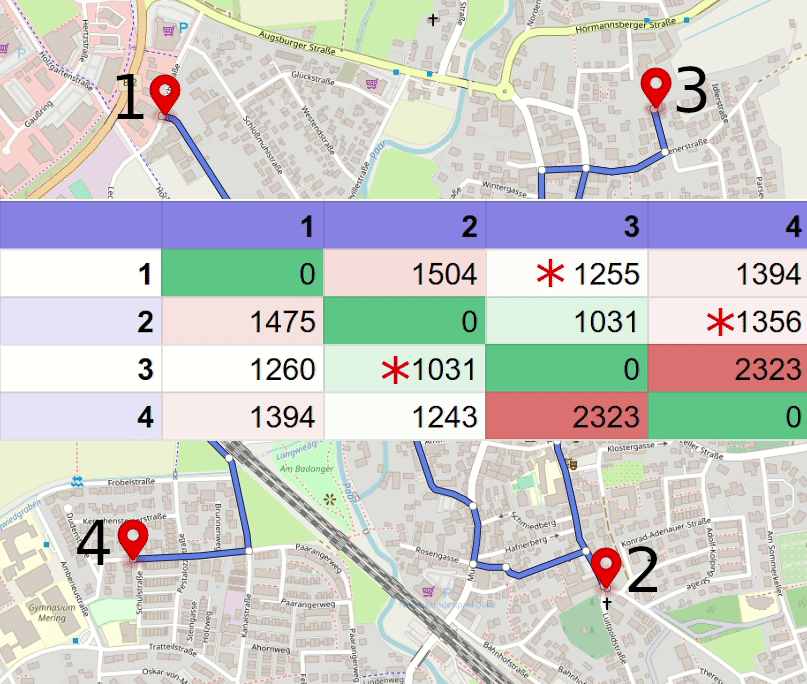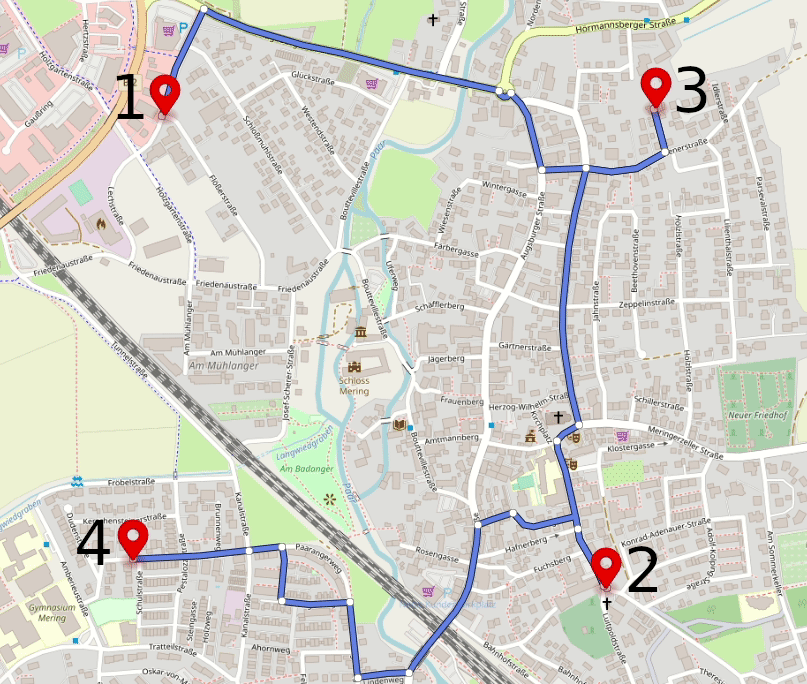
In the example above, routes for each pair of locations can be good enough, but locations visit order is not optimal.
To optimize it, we would need to re-arrange the stops order, and for this, we first need to get or calculate a 4x4 distance matrix. One of the easy ways to get it done is to use Geoapify Matrix API, but for a small number of locations, you can use Routing API or even collect data manually from Google Maps.
As we only have four stops, it is easy to spot the shortest transitions between stops and update the route stop order. More complex scenarios would require software that can take the matrix and calculate the best stop sequence from it. You can use Excel, QGIS, Python Scipy, and many other commercial and open source applications for this.
Drive time matrix for delivery planning
Let's consider a more complex scenario when multiple vehicles need to deliver orders to multiple different customer addresses in an optimal way.
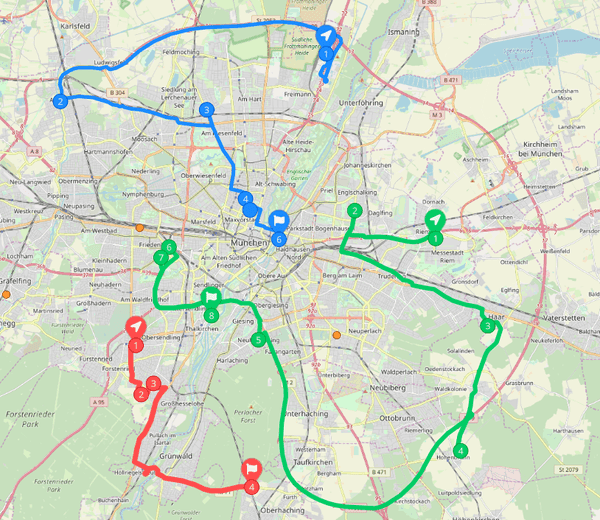
Optimizing complex route planning scenarios often require accounting for delivery schedules, priorities, capacity constraints, and other parameters. Solving such problems with the built-in functionality of applications like Excel or QGIS is hard, and sometimes not feasible.
Most of the time you would need to use special optimization software or APIs, like Geoapify Route Planner API or Google OR-Tools.
Route matrix for reachability analysis
Sometimes optimizing just one or several routes may not be enough, and a more general picture is needed. For example, analyzing travel time of all possible routes originating from a given location.
As displaying many thousands of possible route lines won't be helpful, a "reachability area" visualization is used instead. Reachability area can be defined by so-called "isoline" - a contour around all locations reachable within same time or distance.
One of the good ways to calculate an isoline is based on the calculation of a time-distance matrix for a regular point grid, with a starting location at its center. Each point in the point grid matches a matrix cell and therefore gets a corresponding route time or distance value.
There are several algorithms, including above mentioned Douglas-Peucker, which can be used to generate an isoline from the point grid, by connecting points with similar values.
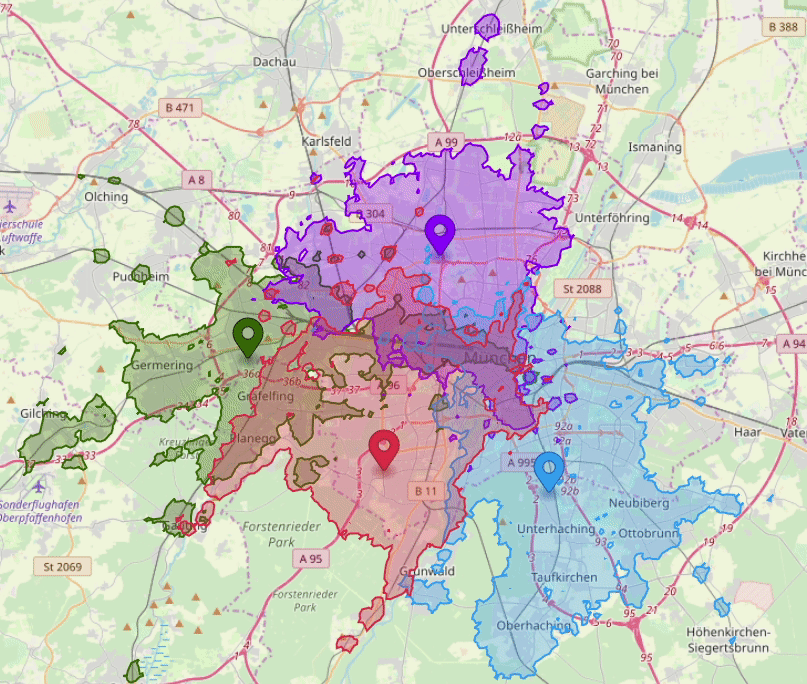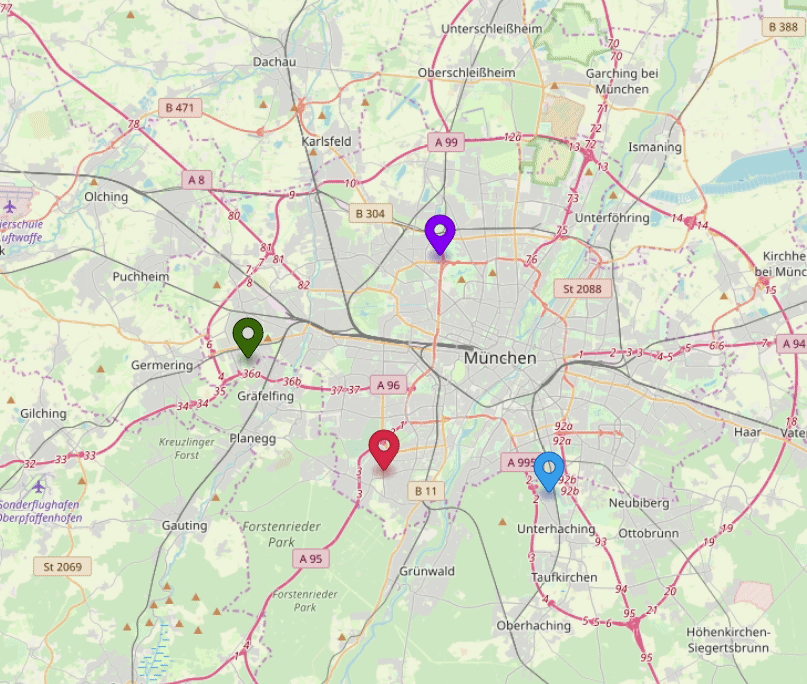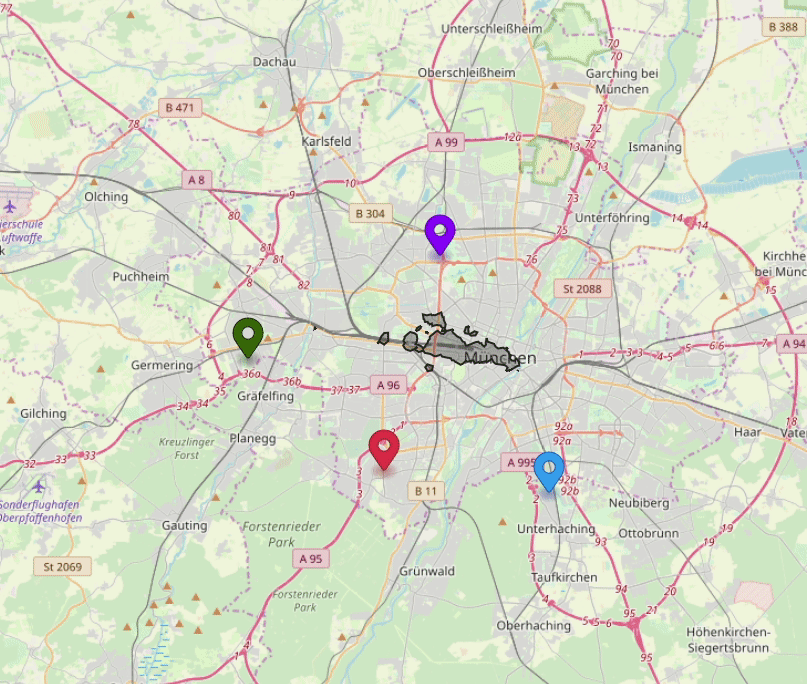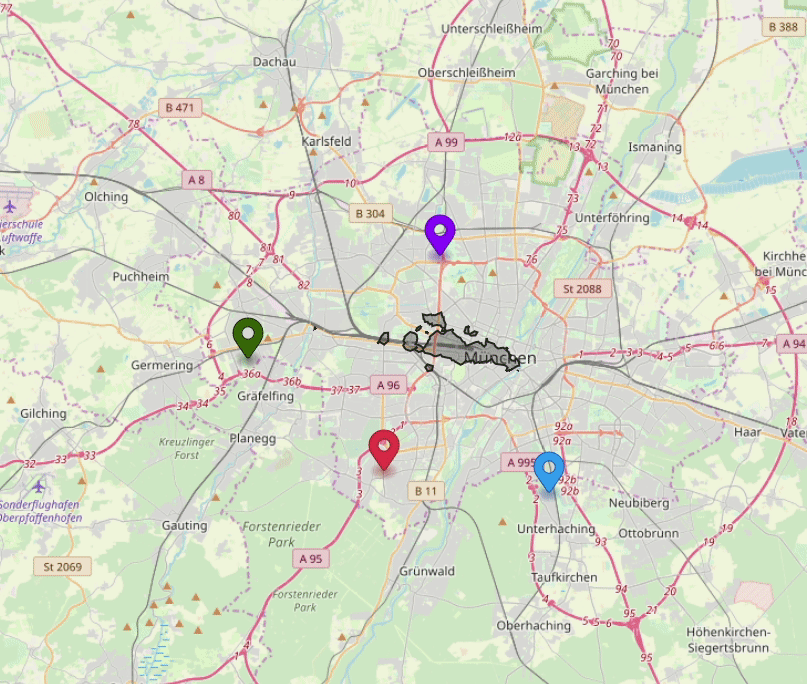
Despite the complexity, isolines and reachability areas can be essential for many analytical tasks. For instance, calculating and optimizing service areas for existing and planned warehouse locations, finding "white spots" in the city public transportation network, and more.
Also, not every task requires a custom route cost matrix or reachability areas. In most cases reachability areas are defined by either "isochrones" (reachability by time), or "isodistances" (reachability by distance). Both are well covered by our Isoline API.
Summary
Route matrix is a core component for solving most route planning and optimization problems. It is often hidden "inside" existing software and APIs, but can be extremely useful if you have additional requirements or building a custom solution.
Geoapify Distance Matrix API is one of the easiest to use and cost-efficient ways to generate route time-distance matrices.